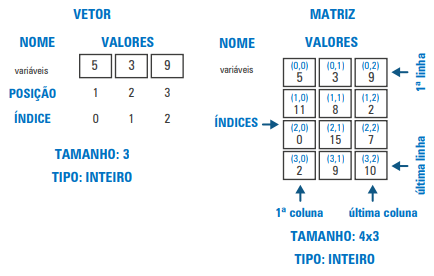
As matrizes expandem o conceito de vetores, que são estruturas unidimensionais (como uma lista). Uma matriz funciona como uma "tabela" bidimensional, com linhas e colunas, sendo ideal para representar problemas que dependem de uma disposição em duas dimensões, como coordenadas em um mapa, peças em um tabuleiro ou até mesmo os pixels de uma imagem.
Enquanto um vetor precisa de apenas um índice para acessar uma posição, uma matriz necessita de dois: um para a linha
e outro para a coluna. A indexação também começa em 0, então a primeira posição de uma matriz é (0,0). A principal
diferença na declaração em C# é o uso de uma vírgula dentro dos colchetes ([,]) para indicar as duas
dimensões.
É possível definir os valores da matriz diretamente em sua criação. A formatação com múltiplas linhas ajuda a visualizar a estrutura, mas não é obrigatória.
double[,] notas = {
{ 8.7, 5.4, 6.2 },
{ 3.8, 2.7, 8.5 },
{ 9.1, 0.9, 4.2 },
{ 7.1, 1.8, 8.8 }
};
Para acessar ou alterar um valor, você deve sempre informar os dois índices (linha e coluna).
// Altera o valor na primeira linha, segunda coluna notas[0, 1] = 6.4; // Copia o valor da última linha e última coluna para uma variável double nota_do_antonio = notas[3, 2];
Você pode declarar uma matriz especificando o número de linhas e colunas, para depois preencher os valores.
double[,] notas = new double[4, 3];
Também é possível declarar a matriz e inicializá-la em outro ponto do código.
double[,] notas; notas = new double[4, 3];
Matrizes são perfeitas para jogos de tabuleiro como xadrez, damas ou, como no exemplo a seguir, Campo Minado.
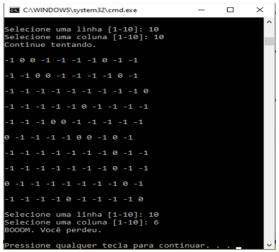
Vamos usar uma matriz 10x10 para o campo, onde `0` é uma posição vazia, `1` é uma bomba e `2` é a bandeira. Outra matriz, `jogo`, registrará as ações do jogador.
Criação e inicialização do campo:
int[,] campo = new int[10, 10]; // Matriz com posições dos elementos do campo
int[,] jogo = new int[10, 10]; // Matriz que registra ações do jogador
int qtdLinhas = campo.GetLength(0);
int qtdColunas = campo.GetLength(1);
// Preenche a matriz 'campo' com 0 e a matriz 'jogo' com -1
for (int l = 0; l < qtdLinhas; l++)
{
for (int c = 0; c < qtdColunas; c++)
{
campo[l, c] = 0;
jogo[l, c] = -1;
}
}
Para percorrer ou preencher uma matriz, a forma padrão é utilizar duas estruturas for, uma dentro da
outra. O laço externo percorre as linhas, e o interno percorre as colunas.
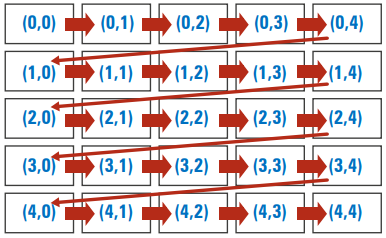
Posicionamento aleatório dos elementos:
// Posicionamento aleatório da bandeira
Random gerador = new Random();
int linha = gerador.Next(qtdLinhas);
int coluna = gerador.Next(qtdColunas);
campo[linha, coluna] = 2;
// Posicionamento aleatório das 5 bombas
int bombasPosicionadas = 0;
do
{
linha = gerador.Next(qtdLinhas);
coluna = gerador.Next(qtdColunas);
if (campo[linha, coluna] == 0)
{
campo[linha, coluna] = 1;
bombasPosicionadas++;
}
} while (bombasPosicionadas < 5);
Loop principal de interação com o jogador:
bool fimJogo = false;
do
{
// Imprime o tabuleiro do jogador
for (int l = 0; l < qtdLinhas; l++)
{
for (int c = 0; c < qtdColunas; c++)
{
Console.Write(string.Format("{0} ", jogo[l, c]));
}
Console.Write(Environment.NewLine + Environment.NewLine);
}
Console.Write("Selecione uma linha [1-10]: ");
linha = Convert.ToInt32(Console.ReadLine()) - 1;
Console.Write("Selecione uma coluna [1-10]: ");
coluna = Convert.ToInt32(Console.ReadLine()) - 1;
switch (campo[linha, coluna])
{
case 0:
jogo[linha, coluna] = 0;
Console.Write("Continue tentando.\n\n");
break;
case 1:
jogo[linha, coluna] = 1;
Console.Write("BOOOM. Você perdeu.\n\n");
fimJogo = true;
break;
default:
jogo[linha, coluna] = 2;
Console.Write("Parabéns. Você ganhou!\n\n");
fimJogo = true;
break;
}
} while (!fimJogo);
Matrizes podem ser passadas como argumentos para funções, assim como os vetores. Uma observação importante é que matrizes (e vetores) são passadas por referência. Isso significa que qualquer alteração feita na matriz dentro da função se refletirá na matriz original, fora da função.
Código principal do jogo:
char[,] tabuleiro = new char[3, 3];
int linha, coluna;
bool fimJogo = false;
int jogador = 1;
int jogada = 0;
// Preenchimento da matriz com espaços em branco
for (int l = 0; l < 3; l++)
for (int c = 0; c < 3; c++)
tabuleiro[l, c] = ' ';
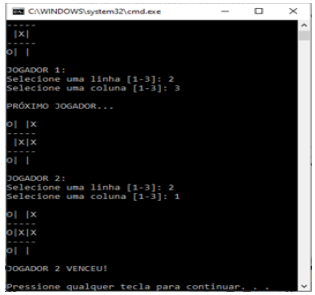
do
{
imprimirTabuleiro(tabuleiro);
if (jogador == 1)
Console.Write("JOGADOR 1:\n");
else
Console.Write("JOGADOR 2:\n");
Console.Write("Selecione uma linha [1-3]: ");
linha = Convert.ToInt32(Console.ReadLine()) - 1;
Console.Write("Selecione uma coluna [1-3]: ");
coluna = Convert.ToInt32(Console.ReadLine()) - 1;
jogada++;
fimJogo = conferirJogada(tabuleiro, linha, coluna, jogador, jogada);
// Troca de jogador
if (jogador == 1)
jogador = 2;
else
jogador = 1;
} while (!fimJogo);
imprimirTabuleiroEsta função apenas lê a matriz e a exibe no console com formatação.
static void imprimirTabuleiro(char[,] tabuleiro)
{
for (int l = 0; l < 3; l++)
{
for (int c = 0; c < 3; c++)
{
Console.Write(string.Format("{0}", tabuleiro[l, c]));
if (c < 2)
Console.Write("|");
}
Console.Write(Environment.NewLine);
if (l < 2)
Console.Write("-----\n");
}
}
conferirJogadaEsta função recebe a jogada, altera o tabuleiro (marcando 'X' ou 'O') e verifica se houve um vencedor ou empate.
static bool conferirJogada(char[,] tabuleiro, int linha, int coluna, int jogador, int jogada)
{
bool trinca = false;
if (jogador == 1)
tabuleiro[linha, coluna] = 'X';
else
tabuleiro[linha, coluna] = 'O';
// Verificar na mesma linha
for (int c = 0; c < 3; c++)
{
if (tabuleiro[linha, c] != tabuleiro[linha, coluna])
break;
if (c == 2)
trinca = true;
}
// Verificar na mesma coluna
if (!trinca)
{
for (int l = 0; l < 3; l++)
{
if (tabuleiro[l, coluna] != tabuleiro[linha, coluna])
break;
if (l == 2)
trinca = true;
}
}
// Verificar na diagonal principal
if (!trinca)
{
if (linha == coluna)
{
for (int cont = 0; cont < 3; cont++)
{
if (tabuleiro[cont, cont] != tabuleiro[linha, coluna])
break;
if (cont == 2)
trinca = true;
}
}
}
// Verificar na diagonal secundária
if (!trinca)
{
if (linha + coluna == 2)
{
for (int cont = 0; cont < 3; cont++)
{
if (tabuleiro[cont, 2 - cont] != tabuleiro[linha, coluna])
break;
if (cont == 2)
trinca = true;
}
}
}
if (trinca)
{
Console.WriteLine();
imprimirTabuleiro(tabuleiro);
Console.Write("JOGADOR " + jogador + " VENCEU!\n\n");
return true;
}
if (jogada == 9)
{
Console.WriteLine();
imprimirTabuleiro(tabuleiro);
Console.Write("EMPATE!\n\n");
return true;
}
else
{
Console.Write("\nPRÓXIMO JOGADOR...\n\n");
return false;
}
}
Veja o seguinte conteúdo para melhor entendimento sobre matrizes multidimensionais: link
for aninhado
dentro de outro.