Algoritmos de Busca em Vetores

Uma das tarefas mais comuns em programação é encontrar uma informação específica dentro de um grande conjunto de dados. Imagine procurar uma palavra em um dicionário: você abriria na primeira página e leria palavra por palavra? Ou abriria no meio e decidiria para que lado ir? Esta aula apresenta duas estratégias para um computador fazer exatamente isso: a busca linear (o método sequencial) e a busca binária (o método inteligente).

1. Busca Linear: A Força Bruta

Como Funciona?

Este é o método mais simples e intuitivo. Ele funciona como um detetive que verifica cada casa de uma rua, uma por uma, começando do número 1, até encontrar o que procura. Em um vetor, o programa começa no índice 0 e avança posição por posição, comparando cada elemento com o valor buscado.

Código C#

int[] dados = { 52, 17, 69, 84, 3, 26, 83, 54, 19, 50 };
int valor_procurado = 54;
bool valor_encontrado = false;

for (int i = 0; i < dados.Length; i++)
{
    if (dados[i] == valor_procurado)
    {
        Console.WriteLine("Valor encontrado no indice " + i);
        valor_encontrado = true;
        break; // Encerra o loop, pois já achamos o valor
    }
}

if (!valor_encontrado)
{
    Console.WriteLine("Valor não encontrado");
}

Análise Rápida

2. Busca Binária: A Estratégia Inteligente

A Regra de Ouro

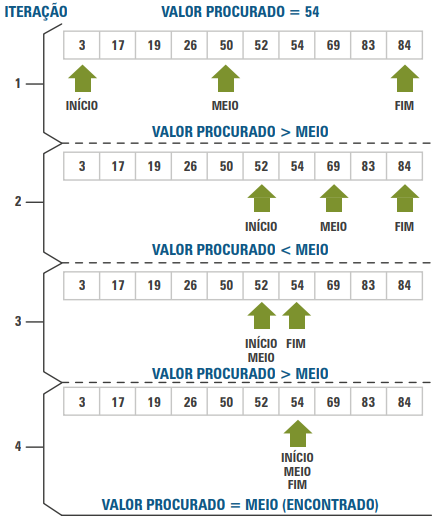
Para a Busca Binária funcionar, há uma condição OBRIGATÓRIA: o vetor precisa estar ordenado (do menor para o maior). Se o vetor estiver desordenado, o algoritmo não funcionará e dará resultados incorretos.

Como Funciona?

Este método usa a estratégia de "divisão e conquista", como ao procurar no dicionário:

  1. Olhe para o elemento que está exatamente no meio do vetor.
  2. Se o valor que você procura for maior que o do meio, você pode ignorar toda a primeira metade do vetor e repetir o processo apenas na metade da direita.
  3. Se for menor, ignore toda a segunda metade e repita o processo na metade da esquerda.
  4. Continue dividindo o problema pela metade a cada passo, até encontrar o valor ou não sobrar mais elementos para verificar.

Exemplo Visual

Exemplo de passo a passo da busca binária

Código C#

int[] dados = { 3, 17, 19, 26, 50, 52, 54, 69, 83, 84 }; // Vetor OBRIGATORIAMENTE ordenado
int valor_procurado = 54;
bool valor_encontrado = false;

int inicio = 0;
int fim = dados.Length - 1;
int meio;

do
{
    meio = inicio + (fim - inicio) / 2; // Calcula o índice do meio
    if (dados[meio] == valor_procurado)
    {
        Console.WriteLine("Valor encontrado no índice " + meio);
        valor_encontrado = true;
        break;
    }
    else if (dados[meio] > valor_procurado)
    {
        fim = meio - 1; // Descarta a segunda metade
    }
    else
    {
        inicio = meio + 1; // Descarta a primeira metade
    }
} while (inicio <= fim);

if (!valor_encontrado)
{
    Console.WriteLine("Valor não encontrado");
}

3. Análise de Algoritmos: Medindo a Eficiência

O que é a Notação "Big O"?

Como podemos provar que um algoritmo é "melhor" que outro de forma objetiva? Usamos uma ferramenta matemática chamada Notação Grande O (Big O). Ela não mede o tempo em segundos, mas sim como a quantidade de operações (a "demora") de um algoritmo cresce à medida que a quantidade de dados de entrada (que chamamos de 'n') aumenta.

Complexidade da Busca Linear: O(n)

Lê-se "O de n". Isso significa que, no pior caso, o número de passos é diretamente proporcional ao número de elementos (`n`). Se o vetor tem 10 elementos, pode levar até 10 verificações. Se tiver 1 milhão de elementos, pode levar até 1 milhão de verificações. O crescimento é linear.

Complexidade da Busca Binária: O(log n)

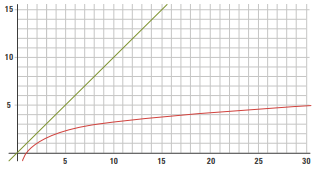
Lê-se "O de log de n". Esta é a grande vantagem. Significa que o número de passos cresce de forma muito lenta. Mesmo que você dobre o número de elementos, o número de passos no pior caso aumenta em apenas um. Para encontrar um item em um vetor com 1 milhão de elementos, a busca binária leva no máximo 20 passos!

Gráfico Comparativo

O gráfico abaixo mostra a diferença: a linha da busca linear (função `n`) sobe de forma íngreme e constante, enquanto a linha da busca binária (função `log n`) fica quase plana, mostrando como ela é mais "escalável" para grandes volumes de dados.

Gráfico comparando a função linear e a logarítmica

Veja o seguinte vídeo para melhor entendimento sobre análise de algoritmos: link

Considerações Finais

A escolha entre os algoritmos depende do seu problema: