Algoritmos Recursivos

A recursividade é uma abordagem para a solução de problemas que envolve a repetição de operações, assim como as estruturas de repetição (laços) que já vimos. A diferença fundamental é que, em vez de um laço, uma função recursiva tem a característica de chamar a si mesma em algum ponto de seu algoritmo. Para que isso não gere um loop infinito, a função precisa ter um critério de parada bem definido, um ponto no qual as chamadas a si mesma são encerradas.

1. Definição de um Problema Recursivo

Para que uma função recursiva funcione corretamente, são necessários alguns elementos essenciais. A ausência de qualquer um deles pode levar a um loop infinito. Os requisitos são:

• Um valor de entrada (parâmetro) para a função.
• Uma operação sobre esse valor de entrada para produzir outro valor.
• Uma chamada para a própria função, passando como argumento um valor diferente do que ela recebeu (geralmente o resultado da operação anterior).
• Um critério de parada (também chamado de caso base), onde a função encerra as chamadas a si mesma e retorna um valor.

Exemplo 1: Fatorial de um Número

O fatorial é a multiplicação de um número por todos os seus antecessores até 1. Para entendermos a recursão, vamos primeiro ver a solução iterativa (com laços).

Solução Iterativa (Fatorial)

Esta função usa um laço while para multiplicar repetidamente o resultado pelo número atual, decrementando o número a cada passo até que ele não seja mais maior ou igual a 1.

public static int fatIterativo(int numero)
{
    int resultado = 1;
    while (numero >= 1)
    {
        resultado = resultado * numero;
        numero = numero - 1;
    }
    return resultado;
}

Solução Recursiva (Fatorial)

A versão recursiva traduz a definição matemática do fatorial (n! = n * (n-1)!) diretamente em código. O critério de parada ocorre quando o número chega a 1 ou 0.

public static int fatRecursivo(int numero)
{
    // Caso Base: a condição de parada.
    if (numero == 1 || numero == 0)
    {
        return 1;
    }
    // Passo Indutivo: a chamada recursiva.
    else
    {
        return numero * fatRecursivo(numero - 1);
    }
}

Exemplo 2: Sequência de Fibonacci

A sequência de Fibonacci começa com os dois primeiros termos valendo 1. A partir do terceiro, cada termo corresponde à soma dos dois anteriores.

Solução Iterativa (Fibonacci)

Nesta função, um laço for começa no terceiro termo e vai até o termo desejado. A cada iteração, o próximo número é calculado como a soma dos dois anteriores, e as variáveis são atualizadas para a próxima iteração.

public static int fibIterativo(int numero)
{
    int num1 = 1;
    int num2 = 1;
    int proxNum = 0;
    for (int i = 3; i <= numero; i++)
    {
        proxNum = num1 + num2;
        num1 = num2;
        num2 = proxNum;
    }
    return proxNum;
}

Solução Recursiva (Fibonacci)

A solução recursiva para Fibonacci pode ser feita passando os valores da sequência como parâmetros. As chamadas cessarão quando o contador (numeroSequencia) chegar a 1, que é o critério de parada. A cada chamada, os parâmetros são atualizados: `numero1` vira `numero2`, e `numero2` vira a soma dos dois anteriores.

public static int fibRecursivo(int numero1, int numero2, int numeroSequencia)
{
    if (numeroSequencia > 1)
    {
        return fibRecursivo(numero2, numero1 + numero2, --numeroSequencia);
    }
    else
    {
        return numero1;
    }
}

2. Estratégia para Escrever um Algoritmo Recursivo

Uma boa estratégia para modelar um problema de forma recursiva é usar o princípio matemático da indução, que se baseia em duas partes:

• Passo Base: A solução para o caso mais simples e fundamental do problema.
• Passo Indutivo: A solução para os demais casos, onde cada caso é expresso em função do caso anterior.

Exemplo 3: Multiplicação usando Soma

Vamos definir a multiplicação de `m * n` usando apenas a operação de adição.

Solução Iterativa (Multiplicação)

A função executa uma repetição `n` vezes, somando o valor de `m` a uma variável de resultado a cada passo.

public static int multIterativa(int m, int n)
{
    int r = 0;
    for (int i = 1; i <= n; i++)
    {
        r += m;
    }
    return r;
}

Definição Indutiva e Solução Recursiva

• Passo Base: O caso mais simples é quando `n` é 0. Qualquer número `m` multiplicado por 0 é 0.
• Passo Indutivo: A multiplicação de `m * n` pode ser definida como `m` somado ao resultado de `m * (n - 1)`.

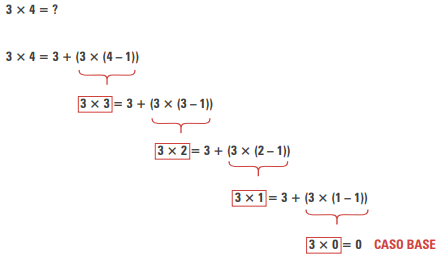
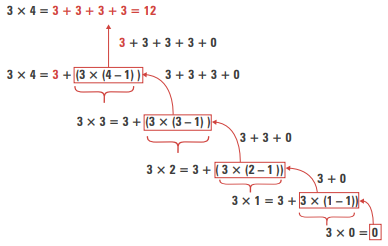
O código recursivo abaixo implementa diretamente essa definição. O bloco if representa o Passo Base, e o bloco else o Passo Indutivo.

public static int multRecursiva(int m, int n)
{
    // Passo Base
    if (n == 0)
    {
        return 0;
    }
    // Passo Indutivo
    else
    {
        return m + multRecursiva(m, n - 1);
    }
}

3. Teste de Mesa para um Algoritmo Recursivo

Um "teste de mesa" é uma forma de simular a execução de um algoritmo no papel para entender seu fluxo e a alteração das variáveis. Em uma função recursiva, a cada nova chamada, o computador aloca mais espaço na memória para as novas variáveis, um processo que pode ser visualizado como um "empilhamento" de execuções.

Quando uma chamada atinge o caso base, ela retorna um valor. Com esse resultado, a chamada anterior pode concluir seu cálculo e retornar seu próprio resultado, sendo "desempilhada" e liberando memória. Esse processo continua até que a chamada original seja resolvida. O alto consumo de memória é uma característica importante das funções recursivas e deve ser considerado.

Veja o seguinte vídeo para melhor entendimento sobre recursividade: link

Considerações Finais

Qualquer problema que pode ser resolvido recursivamente também pode ser resolvido de forma iterativa. A escolha entre uma abordagem e outra depende do contexto.

Vantagens da Recursão

• O código pode ser mais conciso, claro e próximo da notação matemática do problema, facilitando o entendimento.
• É a forma mais natural de resolver problemas que se subdividem em problemas menores e idênticos.

Desvantagens da Recursão

• Geralmente é mais lenta que a iteração, pois cada chamada de função tem um custo de processamento.
• Consome mais memória, pois cada chamada é "empilhada". Um excesso de chamadas pode levar a um erro de estouro de pilha (Stack Overflow).

A recursividade é um conceito fundamental para algoritmos mais avançados que veremos futuramente, que a utilizam para obter maior eficiência.